Luas Kurva Integral

Luas Kurva Integral. Setelah kita mempelajari cara mengintegralkan suatu fungsi baik itu fungsi aljabar maupun fungsi trigonometri sudah saatnya kita akan mempelajari penggunaan integral itu sendiri. Untuk kurva berbentuk linear atau garis lurus luas dapat dicari dengan metode biasa menghitung luas segitiga atau trapesium. Ada beberapa penggunaan dari integral diantaranya yaitu menghitung luas daerah yang dibatasi oleh beberapa kurva menghitung volume benda putar dan menghitung panjang lintasan suatu kurva. Berikut ini merupakan soal dan pembahasan mengenai penentuan luas daerah yang dibatasi oleh kurva dengan menggunakan konsep integral.

Soal Dan Pembahasan Luas Daerah Menggunakan Integral Mathcyber1997 Soal Dan Pembahasan Luas Daerah Menggunakan Integral Mathcyber1997 From mathcyber1997.com

Mio soul 2008 Mimpi orang tua sakit Mining doge gratis tanpa deposit 2019 Mimpi melihat harimau

Langkah pertama yang harus dilakukan adalah mengetahu bentuk gambar fungsi fx dan gx. Luas daerah yang dibatasi oleh kurva y x2 4x 5 dan sumbu x adalah. Integral - Anti Turunan Luas di Bawah Kurva Integral Tentu Integral Tak Tentu Teorema Dasar Kalkulus Dan Aturan Substitusi. Setelah digambar grafiknya membentuk segitiga sehingga konsep menghitung dengan integral bisa diabaikan. Ada beberapa penggunaan dari integral diantaranya yaitu menghitung luas daerah yang dibatasi oleh beberapa kurva menghitung volume benda putar dan menghitung panjang lintasan suatu kurva. Integral-Luas Daerah yang Dibatasi Kurva Contoh Soal dan Pembahasan Intinya pada postingan kali ini saya akan memberikan contoh tentang aplikasi integral dalam menghitung luas daerah yang dibatasi sebuah kurva.

Luas daerah yang dibatasi oleh kurva dapat dihitung menggunakan integral.

Penentuan konsumsi energi di Bandung pada suatu hari. Y 2x 5 dan sumbu x. Contoh Soal dan Pembahasan Integral Sebagai Luas Daerah Kurva Pada bahasan kali ini setelah kalian mempelajari konsep integral sebagai luas daerah. Luas daerah kurva dengan integral 1. Akhir dari proses perhitungan integral tersebut menghasilkan nilai yang mewakili luas daerah. Perlu diperhatikan bahwa integral yang digunakan adalah integral standar bukan integral lipat yang dipelajari pada kalkulus lanjut.

17 Contoh Soal Integral Luas Daerah Antara Dua Kurva Kumpulan Contoh Soal Source: teamhannamy.blogspot.com

Hitunglah luas daerah yang dibatasi oleh garis y x. Penentuan konsumsi energi di Bandung pada suatu hari. Luas daerah yang dibatasi oleh kurva y x2 4x 5 dan sumbu x adalah. Y 2x 5 dan sumbu x. Contoh Soal dan Pembahasan Integral Sebagai Luas Daerah Kurva Pada bahasan kali ini setelah kalian mempelajari konsep integral sebagai luas daerah.

Aplikasi Integral Tentu Untuk Menghitung Luas Daerah Madematika Source: madematika.net

Proses mendapatkan luas daerah yang dibatasi kurva tersebut melalui penggambaran kurva menentukan batas integral dan kemudian melakukan perhitungan integral. Contoh 1 Aplikasi Integral untuk menghitung luas daerah yang dibatasi kurva. Peramalan jumlah populasi pada masa untuk beberapa tahun yang akan datang. Untuk itulah maka kita perlu memahami gambar kurva. Ada beberapa penggunaan dari integral diantaranya yaitu menghitung luas daerah yang dibatasi oleh beberapa kurva menghitung volume benda putar dan menghitung panjang lintasan suatu kurva.

Cara Cepat Menghitung Luas Daerah Berkaitan Integral Konsep Matematika Koma Source: konsep-matematika.com

Luas daerah yang dibatasi oleh kurva dapat dihitung menggunakan integral. Pada artikel ini kita membahas aplikasi atau penggunaan integral lainnya yaitu menentukan panjang busur suatu kurva. Soal 1 Luas daerah yang diarsir pada gambar dapat dinyatakan dengan. Untuk menghitung luas ini kita harus memahami apakah daerah yang dimaksud berada di atas kurva di bawah kurva di atas sumbu x ataupun di bawah sumbu x. Setelah digambar grafiknya membentuk segitiga sehingga konsep menghitung dengan integral bisa diabaikan.

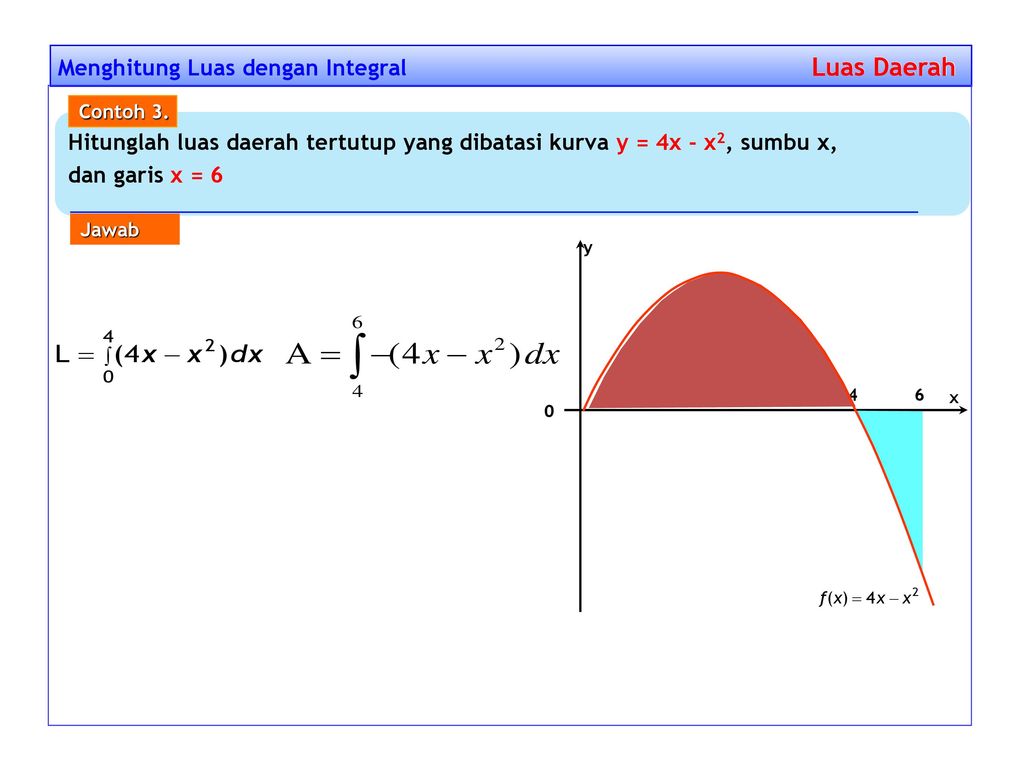Penerapan Integral Menghitung Luas Suatu Daerah Yang Dibatasi Oleh Kurva Dan Sumbu Sumbu Koordinat Ppt Download Source: slideplayer.info

Pada topik kali ini konsep luas daerah yang akan kita pelajari adalah luas daerah yang dibatasi oleh dua fungsi kurva. Integral banyak sekali penggunaanya seperti dalam menghitung luas daerah dibidang datar menggunakan integralmenghitung panjang busur menghitung luas selimut benda putar menghitung volume benda putar Untuk menghitung luas ini kita harus memahami apakah daerah yang dimaksud berada di atas kurva di bawah kurva di atas sumbu x ataupun di bawah sumbu x. Hitunglah luas daerah yang dibatasi oleh garis y x. Ada beberapa penggunaan dari integral diantaranya yaitu menghitung luas daerah yang dibatasi oleh beberapa kurva menghitung volume benda putar dan menghitung panjang lintasan suatu kurva. Sehingga materi yang akan kita bahas adalah Menentukan Panjang Busur dengan Integral.

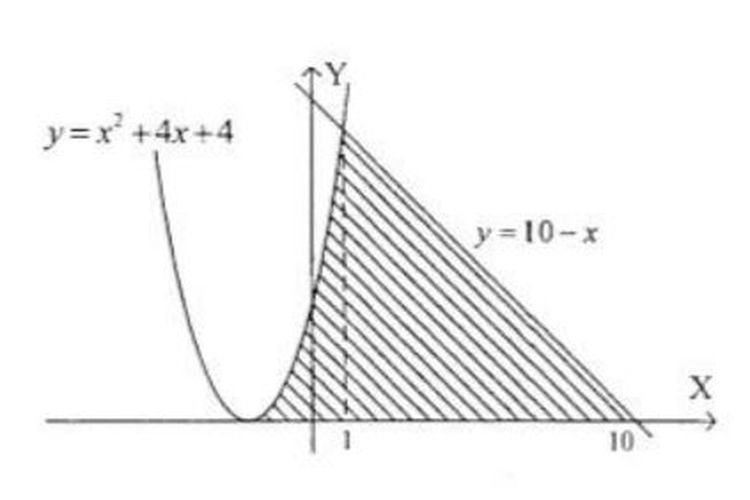Mencari Luas Daerah Yang Diarsir Dengan Integral Halaman All Kompas Com Source: kompas.com

Setelah digambar grafiknya membentuk segitiga sehingga konsep menghitung dengan integral bisa diabaikan. Blog Koma - Setelah kita mempelajari cara mengintegralkan suatu fungsi baik itu fungsi aljabar maupun fungsi trigonometri sudah saatnya kita akan mempelajari penggunaan integral itu sendiri. Jadi luas daerahnya adalah 1 78 satuan luas. Untuk lebih jelasnya perhatikan uraian berikut ini ya. Luas antara dua kurva Secara umum penyelesaian luas daerah dengan menggunakan integral tentu selalu melibatkan batas.

Aplikasi Integral Source: slideshare.net

Perlu diperhatikan bahwa integral yang digunakan adalah integral standar bukan integral lipat yang dipelajari pada kalkulus lanjut. Y 2x 5 dan sumbu x. Blog Koma - Setelah kita mempelajari cara mengintegralkan suatu fungsi baik itu fungsi aljabar maupun fungsi trigonometri sudah saatnya kita akan mempelajari penggunaan integral itu sendiri. Untuk kurva berbentuk linear atau garis lurus luas dapat dicari dengan metode biasa menghitung luas segitiga atau trapesium. Luas daerah yang dibatasi oleh kurva dapat dihitung menggunakan integral.

Menghitung Luas Daerah Menggunakan Integral Konsep Matematika Koma Source: konsep-matematika.com

Silakan dicari rumus luas daerah yang dibatasi oleh 2 buah kurva x1 fy dan x2 gy serta garis y c dan garis y d untuk latihan. Silakan dicari rumus luas daerah yang dibatasi oleh 2 buah kurva x1 fy dan x2 gy serta garis y c dan garis y d untuk latihan. Setelah digambar grafiknya membentuk segitiga sehingga konsep menghitung dengan integral bisa diabaikan. Integral-Luas Daerah yang Dibatasi Kurva Contoh Soal dan Pembahasan Intinya pada postingan kali ini saya akan memberikan contoh tentang aplikasi integral dalam menghitung luas daerah yang dibatasi sebuah kurva. Ada beberapa penggunaan dari integral diantaranya yaitu menghitung luas daerah yang dibatasi oleh beberapa kurva menghitung volume benda putar dan menghitung panjang lintasan suatu kurva.

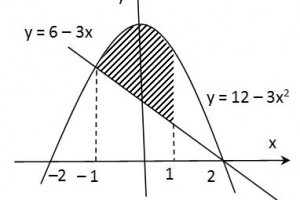Menghitung Luas Daerah Menggunakan Integral Source: utakatikotak.com

Luas antara dua kurva Secara umum penyelesaian luas daerah dengan menggunakan integral tentu selalu melibatkan batas. Salah satu aplikasi integral adalah untuk menghitung luas bidang datar yang dibentuk oleh persamaan-persamaan garis atau kurva Ilustrasi. Blog Koma - Aplikasi integral yang sering dipelajari adalah menghitung luas suatu daerah dan volume benda putar yang dibatasi oleh kurva tertentu. Soal 1 Luas daerah yang diarsir pada gambar dapat dinyatakan dengan. Untuk lebih jelasnya perhatikan kasus-kasus berikut.

Luas Daerah Dengan Integral Youtube Source: youtube.com

Integral banyak sekali penggunaanya seperti dalam menghitung luas daerah dibidang datar menggunakan integralmenghitung panjang busur menghitung luas selimut benda putar menghitung volume benda putar Untuk menghitung luas ini kita harus memahami apakah daerah yang dimaksud berada di atas kurva di bawah kurva di atas sumbu x ataupun di bawah sumbu x. Batas-batas ini ada yang dapat ditentukan dengan mudah hanya dengan dengan melihat sketsa ada juga yang perlu dicari menggunakan bantuan konsep lain seperti konsep sistem persamaan. Proses mendapatkan luas daerah yang dibatasi kurva tersebut melalui penggambaran kurva menentukan batas integral dan kemudian melakukan perhitungan integral. Sekarang kita coba terapkan konsep yang telah kalian pelajari kedalam suatu masalah matematika yang berkaitan dengan integral sebagai luas daerah. Ada beberapa penggunaan dari integral diantaranya yaitu menghitung luas daerah yang dibatasi oleh beberapa kurva menghitung volume benda putar dan menghitung panjang lintasan suatu kurva.

Integral Tentu Penggunaan Integral Materi Rumus Contoh Soal Source: studiobelajar.com

Y 2x 5 dan sumbu x. Ada beberapa penggunaan dari integral diantaranya yaitu menghitung luas daerah yang dibatasi oleh beberapa kurva menghitung volume benda putar dan menghitung panjang lintasan suatu kurva. Hitunglah luas daerah yang dibatasi oleh garis y x. Hitunglah luas daerah yang dibatasi oleh kurva y x ²-2x1 dan garis y x5. Contoh Soal dan Pembahasan Integral Sebagai Luas Daerah Kurva Pada bahasan kali ini setelah kalian mempelajari konsep integral sebagai luas daerah.

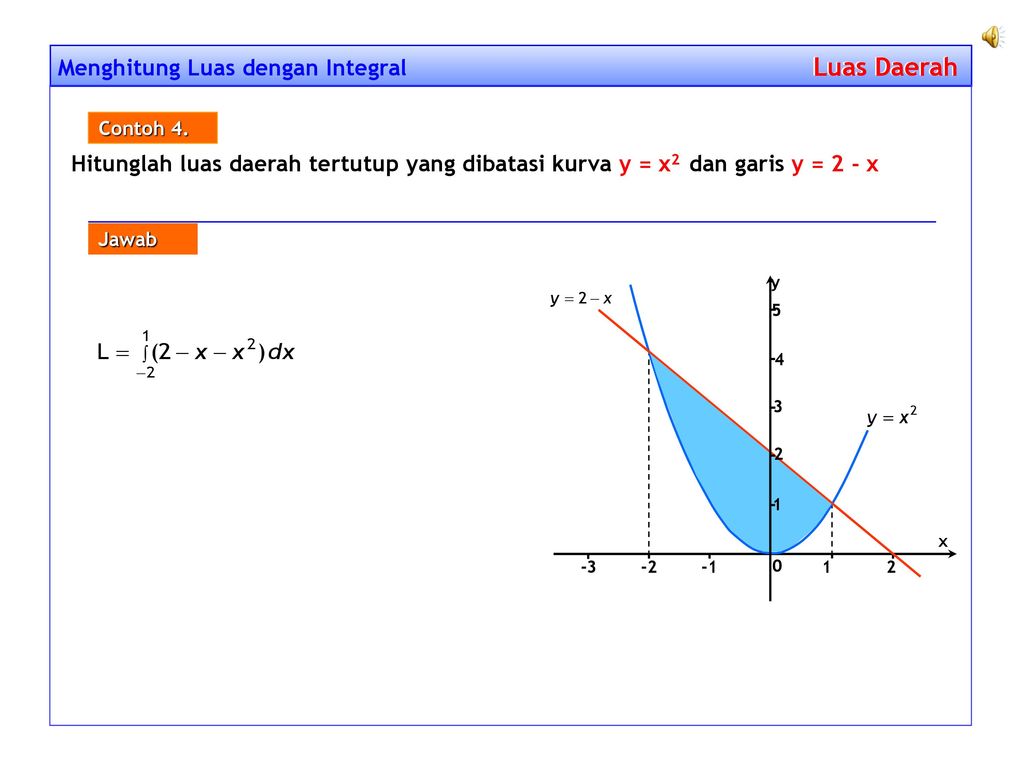Penerapan Integral Menghitung Luas Suatu Daerah Yang Dibatasi Oleh Kurva Dan Sumbu Sumbu Koordinat Ppt Download Source: slideplayer.info

Salah satu aplikasi integral adalah untuk menghitung luas bidang datar yang dibentuk oleh persamaan-persamaan garis atau kurva Ilustrasi. Batas-batas ini ada yang dapat ditentukan dengan mudah hanya dengan dengan melihat sketsa ada juga yang perlu dicari menggunakan bantuan konsep lain seperti konsep sistem persamaan. Langkah pertama yang harus dilakukan adalah mengetahu bentuk gambar fungsi fx dan gx. Ada beberapa penggunaan dari integral diantaranya yaitu menghitung luas daerah yang dibatasi oleh beberapa kurva menghitung volume benda putar dan menghitung panjang lintasan suatu kurva. Luas daerah kurva dengan integral 1.

Integral Luas Daerah Youtube Source: youtube.com

Y 2x 5 dan sumbu x. Pada topik kali ini konsep luas daerah yang akan kita pelajari adalah luas daerah yang dibatasi oleh dua fungsi kurva. Salah satu aplikasi integral adalah untuk menghitung luas bidang datar yang dibentuk oleh persamaan-persamaan garis atau kurva Ilustrasi. Peramalan jumlah populasi pada masa untuk beberapa tahun yang akan datang. Integral-Luas Daerah yang Dibatasi Kurva Contoh Soal dan Pembahasan Intinya pada postingan kali ini saya akan memberikan contoh tentang aplikasi integral dalam menghitung luas daerah yang dibatasi sebuah kurva.

Luas Daerah Integral Youtube Source: youtube.com

Pada topik kali ini konsep luas daerah yang akan kita pelajari adalah luas daerah yang dibatasi oleh dua fungsi kurva. Pada topik kali ini konsep luas daerah yang akan kita pelajari adalah luas daerah yang dibatasi oleh dua fungsi kurva. Luas antara dua kurva Secara umum penyelesaian luas daerah dengan menggunakan integral tentu selalu melibatkan batas. Integral banyak sekali penggunaanya seperti dalam menghitung luas daerah dibidang datar menggunakan integralmenghitung panjang busur menghitung luas selimut benda putar menghitung volume benda putar Untuk menghitung luas ini kita harus memahami apakah daerah yang dimaksud berada di atas kurva di bawah kurva di atas sumbu x ataupun di bawah sumbu x. Sekarang kita coba terapkan konsep yang telah kalian pelajari kedalam suatu masalah matematika yang berkaitan dengan integral sebagai luas daerah.

Contoh Soal Integral Luas Daerah Dan Penyelesaiannya Dapatkan Contoh Source: dapatkancontoh.blogspot.com

Untuk lebih jelasnya perhatikan kasus-kasus berikut. Ada beberapa penggunaan dari integral diantaranya yaitu menghitung luas daerah yang dibatasi oleh beberapa kurva menghitung volume benda putar dan menghitung panjang lintasan suatu kurva. Untuk kurva berbentuk linear atau garis lurus luas dapat dicari dengan metode biasa menghitung luas segitiga atau trapesium. Sekarang kita coba terapkan konsep yang telah kalian pelajari kedalam suatu masalah matematika yang berkaitan dengan integral sebagai luas daerah. Perlu diperhatikan bahwa integral yang digunakan adalah integral standar bukan integral lipat yang dipelajari pada kalkulus lanjut.

Soal Dan Pembahasan Luas Daerah Menggunakan Integral Mathcyber1997 Source: mathcyber1997.com

Posisi dua kurva ini menentukan rumus integral yang akan digunakan. Setelah kita mempelajari cara mengintegralkan suatu fungsi baik itu fungsi aljabar maupun fungsi trigonometri sudah saatnya kita akan mempelajari penggunaan integral itu sendiri. Untuk kurva berbentuk linear atau garis lurus luas dapat dicari dengan metode biasa menghitung luas segitiga atau trapesium. Blog Koma - Aplikasi integral yang sering dipelajari adalah menghitung luas suatu daerah dan volume benda putar yang dibatasi oleh kurva tertentu. Untuk menghitung luas ini kita harus memahami apakah daerah yang dimaksud berada di atas kurva di bawah kurva di atas sumbu x ataupun di bawah sumbu x.

Contoh Soal Integral Luas Daerah Dan Pembahasannya Ops Sekolah Kita Source: opssekolahkita.com

Luas antara dua kurva Secara umum penyelesaian luas daerah dengan menggunakan integral tentu selalu melibatkan batas. Integral-Luas Daerah yang Dibatasi Kurva Contoh Soal dan Pembahasan Intinya pada postingan kali ini saya akan memberikan contoh tentang aplikasi integral dalam menghitung luas daerah yang dibatasi sebuah kurva. Sehingga materi yang akan kita bahas adalah Menentukan Panjang Busur dengan Integral. Setelah kita mempelajari cara mengintegralkan suatu fungsi baik itu fungsi aljabar maupun fungsi trigonometri sudah saatnya kita akan mempelajari penggunaan integral itu sendiri. Jadi luas daerahnya adalah 1 78 satuan luas.

Tutorial Integral Menghitung Luas 1 Matematika Sma Youtube Source: youtube.com

Luas daerah yang dibatasi oleh kurva y x2 4x 5 dan sumbu x adalah. Ada beberapa penggunaan dari integral diantaranya yaitu menghitung luas daerah yang dibatasi oleh beberapa kurva menghitung volume benda putar dan menghitung panjang lintasan suatu kurva. Sekarang kita coba terapkan konsep yang telah kalian pelajari kedalam suatu masalah matematika yang berkaitan dengan integral sebagai luas daerah. Untuk kurva berbentuk linear atau garis lurus luas dapat dicari dengan metode biasa menghitung luas segitiga atau trapesium. Pada artikel ini kita membahas aplikasi atau penggunaan integral lainnya yaitu menentukan panjang busur suatu kurva.

Integral Luas Daerah Yang Dibatasi Kurva Contoh Soal Dan Pembahasan Source: sheetmath.com

Akhir dari proses perhitungan integral tersebut menghasilkan nilai yang mewakili luas daerah. Soal 1 Luas daerah yang diarsir pada gambar dapat dinyatakan dengan. Ada beberapa penggunaan dari integral diantaranya yaitu menghitung luas daerah yang dibatasi oleh beberapa kurva menghitung volume benda putar dan menghitung panjang lintasan suatu kurva. Blog Koma - Setelah kita mempelajari cara mengintegralkan suatu fungsi baik itu fungsi aljabar maupun fungsi trigonometri sudah saatnya kita akan mempelajari penggunaan integral itu sendiri. Y 2x 5 dan sumbu x.

This site is an open community for users to submit their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.

If you find this site helpful, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title luas kurva integral by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.