Tentukan Kardinalitas Himpunan Himpunan Berikut. Mari kita tentukan kardinalitas dari himpunan A dan himpunan B terlebih dahulu ya. A A adalah himpunan bagian dari A itu sendiri yaitu A A. Himpunan set merupakan contoh khusus dari suatu multiset yang dalam hal ini multiplisitas setiap elemennya adalah 0 atau 1. Contoh Kardinalitas Himpunan Untuk lebih jelasnya berikut contoh dari kardinalitas himpunan.
Teori Himpunan
Teori Himpunan From slideshare.net
Klasifikasi bunga mawar putih Kliping tentang olahraga Kliping budaya indonesia Kode aktivasi mandiri syariah
Karena kardinalitas kedua himpunan sama maka himpunan A ekuivalen dengan himpunan B. Berdasarkan kompetensi dasar kurikulum terbaru. Kardinalitas Jumlah elemen di dalam A disebut kardinal dari himpunan A. Contoh soal himpunan semesta Tentukan tiga himpunan semesta yang mungkin dari himpunan berikut. Mari kita tentukan kardinalitas dari himpunan A dan himpunan B terlebih dahulu ya. Jika tidak demikian maka A B.
Banyak anggota himpunan kuasa A adalah 2 pangkat banyak anggota himpunan A.
BAB I HIMPUNAN 3 13 K EANGGOTAAN HIMPUNAN Pada dasarnya himpunan dipakai untuk mengelompokan anggota yang sejenis atau memiliki sifat yang mirip saja tapi bila dipakai untuk menyatakan himpunan dari himpunan lain atau. Contoh Kardinalitas Himpunan Untuk lebih jelasnya berikut contoh dari kardinalitas himpunan. Banyak anggota himpunan kuasa A adalah 2 pangkat banyak anggota himpunan A. Jika diketahui Aabc maka PA adalah himpunan yang anggotanya merupakan semua himpunan. A A adalah himpunan bagian dari A itu sendiri yaitu A A. A x x 4 dan x 10 x bil.
Tentukan Kardinalitas Himpunan Himpunan Berikut A 1 2 3 4 B A I U E O Brainly Co Id
Source: brainly.co.id
Jika A adalah himpunan semua bilangan bulat positif yang membagi habis bilangan 2015 tentukan banyak himpunan bagian dari A yang tidak kosong 15. BAB I HIMPUNAN 3 13 K EANGGOTAAN HIMPUNAN Pada dasarnya himpunan dipakai untuk mengelompokan anggota yang sejenis atau memiliki sifat yang mirip saja tapi bila dipakai untuk menyatakan himpunan dari himpunan lain atau. Jika dan hanya jika setiap unsur A merupakan unsur B dan sebaliknya setiap unsur B merupakan unsur A. A 1 3 5 7 9 nA 5. Tentukan banyaknyaanggota himpunan kuasa A B C dan D.
Bab 1 Himpunan Bagian Ppt Download
Source: slideplayer.info
A 1 3 5 7 9 nA 5. Berikut ini adalah Soal Kardinalitas Himpunansifat himpunan dan Pembahasannya. Berdasarkan kompetensi dasar kurikulum terbaru. A 123 B abc Maka. Tuliskan kardinalitas himpunan Z xx ϵ himp bil bulat x 2 2 6 3.
Tentukan Kardinalitas Himpunan Himpunan Berikut Brainly Co Id
Source: brainly.co.id
A 1 3 5 7 9 nA 5. S x 2 x 12 A 3 5 7 9 11 Tentukan komplemen dari himpunan A. BAB I HIMPUNAN 3 13 K EANGGOTAAN HIMPUNAN Pada dasarnya himpunan dipakai untuk mengelompokan anggota yang sejenis atau memiliki sifat yang mirip saja tapi bila dipakai untuk menyatakan himpunan dari himpunan lain atau. Dua himpunan atau lebih yang memiliki bilangan kardinal sama disebut sederajat. Kardinalitas Jumlah elemen di dalam A disebut kardinal dari himpunan A.
Kardinalitas Dan Operasi Dua Himpunan
Source: slideshare.net
Tentukan kardinalitas himpunan himpunan berikut - 437889 Pembuatan keripik pisang pada suatu industri rumahan dilakukan melalui dua tahap yaitu tahap pengupasan pisang mentah dilanjutkan dengan tahap penggo. Dua himpunan atau lebih yang memiliki bilangan kardinal sama disebut sederajat. A himpunan kosong d. Diketahui semesata dari sebuah himpunan dan himpunan A sebagai berikut. S x 2 x 12 A 3 5 7 9 11 Tentukan komplemen dari himpunan A.
Himpunan Matematika Kelas 7 Bse Kurikulum 2013 Revisi 2016 Lat 2 5 No3 Himpunan Kuasa 1 2 3 4 Youtube
Source: youtube.com
Koplemen dari himpunan A adalah anggota semesta yang bukan anggota dari A. Jika tidak demikian maka A B. Diketahui semesata dari sebuah himpunan dan himpunan A sebagai berikut. Kerbau sapi kambing Penyelesaian. A himpunan kosong d.
Himpunan Matematika Kelas 7 Bse Kurikulum 2013 Revisi 2016 Lat 2 3 No 6 Semesta Himpunan Youtube
Source: youtube.com
S bilangan prima atau. Tentukan himpunan kuasa dari himpunana - himpunan berikut. Karena kardinalitas kedua himpunan sama maka himpunan A ekuivalen dengan himpunan B. Banyak anggota himpunan kuasa A adalah 2 pangkat banyak anggota himpunan A. BAB I HIMPUNAN 3 13 K EANGGOTAAN HIMPUNAN Pada dasarnya himpunan dipakai untuk mengelompokan anggota yang sejenis atau memiliki sifat yang mirip saja tapi bila dipakai untuk menyatakan himpunan dari himpunan lain atau.
1 Tentukan Kardinalitas Dari A Adalah Himpunan Huruf Pembentuk Kata Matematika2 Dik Brainly Co Id
Source: brainly.co.id
Contoh Kardinalitas Himpunan Untuk lebih jelasnya berikut contoh dari kardinalitas himpunan. HIMPUNAN LEPAS DAN BERSENDI Suatu himpunan disebut bersendi jika himpunan-hipunan tersebut memiliki unsur yang sama. Koplemen dari himpunan A adalah anggota semesta yang bukan anggota dari A. B a i u e o nB 5. Mulai dari pengertian sampai jenisnya yaitu himpunan semesta himpunan bagian dan himpunan bagian sejati.
12 Tentukan Kardinalitas Lihat Cara Penyelesaian Di Qanda
Source: qanda.ai
NPA2 nA Contohnya jika nA3 maka nPA2 3 8 jika nB5 maka nPB2 5 32. Mulai dari pengertian sampai jenisnya yaitu himpunan semesta himpunan bagian dan himpunan bagian sejati. Contoh Kardinalitas Himpunan Untuk lebih jelasnya berikut contoh dari kardinalitas himpunan. Satu ke Satu one to one setiat entitas pada himpunan A berhubungan dengan paling banyak dengan satu entitas pada himpunan entitas begitu juga sebaliknya entitas pada himpunan entitas B berhubungan dengan paling banyak dengan satu entitas pada himpunan entitas B. Tentukan banyaknyaanggota himpunan kuasa A B C dan D.
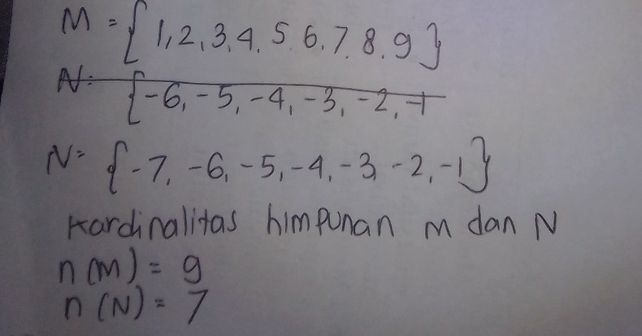1 Jika 1 Xx10x Bilangan Descubre Como Resolverlo En Qanda
Source: qanda.ai
Berikut ini adalah Soal Kardinalitas Himpunansifat himpunan dan Pembahasannya. S bilangan prima atau. Koplemen dari himpunan A adalah anggota semesta yang bukan anggota dari A. A 123 B abc Maka. NPA2 nA Contohnya jika nA3 maka nPA2 3 8 jika nB5 maka nPB2 5 32.
Teori Himpunan
Source: slideshare.net
Jika A adalah himpunan semua bilangan bulat positif yang membagi habis bilangan 2015 tentukan banyak himpunan bagian dari A yang tidak kosong 15. Jika dan hanya jika setiap unsur A merupakan unsur B dan sebaliknya setiap unsur B merupakan unsur A. BAB I HIMPUNAN 3 13 K EANGGOTAAN HIMPUNAN Pada dasarnya himpunan dipakai untuk mengelompokan anggota yang sejenis atau memiliki sifat yang mirip saja tapi bila dipakai untuk menyatakan himpunan dari himpunan lain atau. Berdasarkan kompetensi dasar kurikulum terbaru. Satu ke Satu one to one setiat entitas pada himpunan A berhubungan dengan paling banyak dengan satu entitas pada himpunan entitas begitu juga sebaliknya entitas pada himpunan entitas B berhubungan dengan paling banyak dengan satu entitas pada himpunan entitas B.
Tolong Sya Matematika Susah Skli Bngttt Aku Takut Di Marahin Guru Ya Alaah Tlong Hamba Mu Ini Ya Brainly Co Id
Source: brainly.co.id
Dalam kesempatan berikut kak Hinda akan mengajak semuanya untuk belajar tentang himpunan secara menyeluruh. NPA2 nA Contohnya jika nA3 maka nPA2 3 8 jika nB5 maka nPB2 5 32. Jika A adalah himpunan semua bilangan bulat positif yang membagi habis bilangan 2015 tentukan banyak himpunan bagian dari A yang tidak kosong 15. Berikut ini adalah Soal Kardinalitas Himpunansifat himpunan dan Pembahasannya. N B dan disebut sederajat.
12 Tentukan Kardinalitas Lihat Cara Penyelesaian Di Qanda
Source: qanda.ai
Banyak anggota himpunan kuasa A adalah 2 pangkat banyak anggota himpunan A. A 2 4 6 8 10 12. Tentukan himpunan kuasa dari himpunana - himpunan berikut. Kerbau sapi kambing Penyelesaian. Tentukan banyaknyaanggota himpunan kuasa A B C dan D.
Himpunan Matematika Kelas 7 Bse Kurikulum 2013 Revisi 2016 Lat 2 6 No12 Kardinalitas Youtube
Source: youtube.com
Nyatakan notasi dan anggota himpunan-himpunan berikut dengan tabular form bentuk daftar. Periksa apakah himpunan berikut merupakan basis bagi polinom orde 2 P2 4 6x x2 1 4x 2x2 5 2x x2 4 x 3x2 6 5x 2x2 8 4x x2 Periksa apakah J merupakan subruang dari ruang vektor Polinom orde dua Jika ya tentukan basisnya 5. Diketahui semesata dari sebuah himpunan dan himpunan A sebagai berikut. B Himpunan kosong merupakan himpunan bagian dari A A. Tentukan himpunan kuasa dari himpunana - himpunan berikut.
Volls Uall W 12 Tentukan Kardinalitas Himpunan Himpunan Berikuta A 1 2 3 4 B B A I U E Brainly Co Id
Source: brainly.co.id
A himpunan kosong d. Tentukan banyaknyaanggota himpunan kuasa A B C dan D. Jika dan hanya jika setiap unsur A merupakan unsur B dan sebaliknya setiap unsur B merupakan unsur A. Jika tidak demikian maka A B. Dua himpunan atau lebih yang memiliki bilangan kardinal sama disebut sederajat.
Tentukan Kardinalitas Dari Himpunan Di Bawah Ini A K 2 1 0 1 2 B L 1 Lt 9 B Brainly Co Id
Source: brainly.co.id
Nyatakan notasi dan anggota himpunan-himpunan berikut dengan tabular form bentuk daftar. Kardinalitas suatu multiset didefinisikan sebagai kardinalitas himpunan. Tentukan semua kemungkinan himpunan C. Elemen tersebut pada himpunan ganda. Tuliskan kardinalitas himpunan Z xx ϵ himp bil bulat x 2 2 6 3.
Tentukan Kardinalitas Dari Himpunan Berikut A Himpunan Sb Himpunan Ac Himpunan Bd Himpunan C Brainly Co Id
Source: brainly.co.id
Koplemen dari himpunan A adalah anggota semesta yang bukan anggota dari A. S x 2 x 12 A 3 5 7 9 11 Tentukan komplemen dari himpunan A. Untuk menyatakan A B yang perlu dibuktikan adalah A adalah himpunan bagian dari B dan B merupakan himpunan bagian dari A. Berdasarkan kompetensi dasar kurikulum terbaru. Berikut ini adalah cara menentukan daerah himpunan penyelesaian dari sistem pertidaksamaan linier.
Himpunan Matematika Kelas 7 Bse Kurikulum 2013 Revisi 2016 Lat 2 6 No12 Kardinalitas Youtube
Source: youtube.com
Mulai dari pengertian sampai jenisnya yaitu himpunan semesta himpunan bagian dan himpunan bagian sejati. A himpunan kosong d. Karena kardinalitas kedua himpunan sama maka himpunan A ekuivalen dengan himpunan B. Jika diketahui Aabc maka PA adalah himpunan yang anggotanya merupakan semua himpunan. Mari kita tentukan kardinalitas dari himpunan A dan himpunan B terlebih dahulu ya.
Perhatikan Diagram Venn Berikut A Tentukanlah Kardinalitas Himpunan S Himpunan A Dan Himpunan Brainly Co Id
Source: brainly.co.id
A 1 3 5 7 9 nA 5. Satu ke Satu one to one setiat entitas pada himpunan A berhubungan dengan paling banyak dengan satu entitas pada himpunan entitas begitu juga sebaliknya entitas pada himpunan entitas B berhubungan dengan paling banyak dengan satu entitas pada himpunan entitas B. Mari kita tentukan kardinalitas dari himpunan A dan himpunan B terlebih dahulu ya. Tentukan daerah penyelesaian dari pertidaksamaan 3x-2y leq -6. Tentukan himpunan kuasa dari himpunana - himpunan berikut.
This site is an open community for users to share their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site adventageous, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title tentukan kardinalitas himpunan himpunan berikut by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.